Question

We are standing on the top of a 320 foot tall building and launch a small object upward. The object's vertical altitude, measured in feet, after t seconds is h ( t ) = − 16 t 2 + 128 t + 320 . What is the highest altitude that the object reaches?

Answer 1

The highest altitude that the object reaches is 576 feet.

Explanation:

The maximum altitude reached by the object can be found by using the first and second derivatives of the given function. (First and Second Derivative Tests). Let be
`h(t) = -16\cdot t^(2) + 128\cdot t + 320`, the first and second derivatives are, respectively:

First Derivative

`h'(t) = -32\cdot t +128`

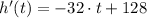
Second Derivative

`h''(t) = -32`

Then, the First and Second Derivative Test can be performed as follows. Let equalize the first derivative to zero and solve the resultant expression:

`-32\cdot t +128 = 0`

`t = (128)/(32)\,s`

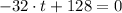
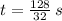
`t = 4\,s` (Critical value)

The second derivative of the second-order polynomial presented above is a constant function and a negative number, which means that critical values leads to an absolute maximum, that is, the highest altitude reached by the object. Then, let is evaluate the function at the critical value:

`h(4\,s) = -16\cdot (4\,s)^(2)+128\cdot (4\,s) +320`

`h(4\,s) = 576\,ft`

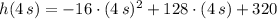
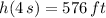
The highest altitude that the object reaches is 576 feet.