Question

A 6 foot person casts a 26 foot shadow. What is the angle of elevation of the sun? (nearest whole degree)

Answer 1

13°

Explanation:

The trigonometric ratio formula can be used in calculating the angle of elevation (x°) of the sun, as the person makes a right angle with the ground.

The height of the person would be the opposite length = 6 ft, the shadow of the person would be the adjacent length = 26 ft

Therefore, according to the trigonometric ratio formula, we would calculate angle of elevation (x°) as follows:

`tan x = (opposite)/(adjacent)`

`tan x = (6)/(26)`

`tan x = 0.2308`

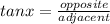
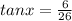
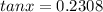
x = tan-¹(0.2308)

x = 12.996

x ≈ 13° (to the nearest whole degree)

The angle of elevation of the sun = 13°