Answer:
Choice C.
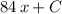 .
.
Explanation:
Consider the power rule for integration. Let
 be a real number that is not equal to
be a real number that is not equal to
 . The power rule for integration states that:
. The power rule for integration states that:
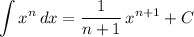 ,
,
How could this rule apply to this question, since there's apparently no
 (or its powers) in the integrand? Keep in mind that
(or its powers) in the integrand? Keep in mind that
 for all real (and particularly non-zero) values of
for all real (and particularly non-zero) values of
 . In other words, the integrand
. In other words, the integrand
 is equal to
is equal to
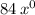 . The integral becomes:
. The integral becomes:
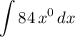 .
.
The constant can be moved outside the integral sign. Therefore:
 .
.
Now that resembles the power rule. In particular,
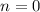 , such that
, such that
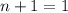 . By the power rule:
. By the power rule:
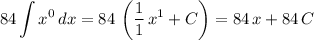 .
.
The non-zero constant in front of
 can be ignored (where
can be ignored (where
 represents the constant of integration.) Therefore:
represents the constant of integration.) Therefore:
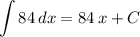 .
.