Question

Find the odds for and the odds against the event rolling a fair die and getting a 4, a 2, or a 1.

Answer 1

Answer: Both in favor and against: 3/6 OR 1/2 OR 50%.

Step-by-step explanation: Both in favor and against: 3/6 OR 1/2 OR 50%.

The probability of rolling one die and getting any digit is
`(1)/(6)`. That is because the desired outcome is only 1 digit out of the 6 total digits on each of the six sides.

That means the probability of rolling either a 1, a 2, or a 4 if you are looking for any of those numbers specifically, is
`(1)/(6)`. But! You are looking to roll a 1, a 2, or a 4, without any preference among those three. Therefore, you are going to add the desired outcomes.

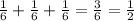`(1)/(6) + (1)/(6) + (1)/(6) = (3)/(6) = (1)/(2)` = 0.5 = 50%

Above, are added the probability of rolling a 1 PLUS the probability of rolling a 2 PLUS the probability of rolling a 4, yielding a 50% probability.

Think about it. There are six total digits on a die. You are okay with rolling three of those. Three is half of six. Therefore, the probability of rolling the number you'd like is one-half, fifty-percent.

Likewise, since the probability of all complement events happening is 1 (or 100%), The odds against rolling either 1, 2, or 4 is also fifty-percent. 100% (which is rolling any number on a die) MINUS 50% (which is rolling a 1, a 2, or a 4 with no preference) EQUALS TO 50% (which is rolling a 3, a 5, or a 6).