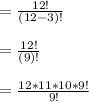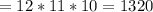Answer:
1320 sets
Explanation:
This problem brothers on selection without repetition, so we will be using permutation to solve this problem.
Given
n= 12 ,which is the number we are choosing from
r= 3, which is the number of committee(president, vice-president, and secretary-treasurer.)
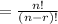
Substituting we have