Question

-4x-7+10x=-7+6x−4x−7+10x=−7+6xminus, 4, x, minus, 7, plus, 10, x, equals, minus, 7, plus, 6, x Choose 1 answer: Choose 1 answer: (Choice A) A No solutions (Choice B) B Exactly one solution (Choice C) C Infinitely many solutions

Answer 1

C Infinitiy solutions

Explanation:

Answer 2

(Choice C) C Infinitely many solutions.

Explanation:

First of all, let us learn about solutions of linear equations in one variable.

The linear equations in one variable usually have one solution.

For example:

`2x =x+3`

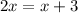
When we solve this:

`2x-x=3\\\Rightarrow x=3`

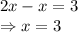
One solution is
`x = 3`

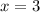
But there can be situations when there are

1. No solutions:

For example:

`x =x+9`

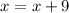
It means that value x is equal to value of x+9 which can never be true.

Truth is the term on Right Hand Side is always 9 greater than the value of Left Hand Side.

Such situations are called Contradictions.

Here, no solution exists.

2. Infinitely many solutions:

For example:

`x+2x+8=3x+8`

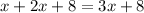
The Right hand Side is just the simplification of the LHS.

And LHS is always equal to RHS no matter what is the value of variable
`x`.

It means there are infinitely many solutions for this equation.

-----------------------------------------------------

Now, let us have a look at the given equation in the question:

`-4x-7+10x=-7+6x`

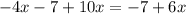
Taking LHS:
`-4x-7+10x`

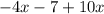
Taking the terms with
`x` on one side:

`-7+10x-4x\\\Rightarrow -7+6x`

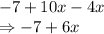
which is equal to Right Hand Side.

Hence, as we discussed in case 2 above.

For every value of
`x` the equation holds true.

`\therefore` There exists infinitely many solutions to the given equation.

Correct answer is:

(Choice C) C Infinitely many solutions