Question

3.

Which of the following describes the parabola with the equation y = -x2 – 3x + 6?
A. The axis of symmetry is x = -1.5 and the vertex is (-1.5, 8.25).
B. The axis of symmetry is x = -1 and the vertex is (-1, -3).
C. The axis of symmetry is x = 0 and the vertex is (0, 6).
D. The axis of symmetry is x = 1.5 and the vertex is (1.5, 12.75).

Answer 1

Hello Papi :D

I will solve the problem by applying the perfect square trinomial. In this way we obtain the canonical form. Another way would be to derive the function, but I don't know if you're familiar with it.

`f(x)=-{x}^(2)-3x+6`

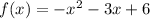
First: let us take out the common factor:
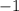`-1`, since we remember that the canonical form is characterized as follows:

Then, it remains:

`f(x)=-1({x}^(2)+3x-6)`

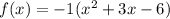
Then: the coefficient of the variable
`x` We divided it between
`2`, And we square it (they will be one positive and one negative). In our case:

`(3)/(2)\rightarrow {(3)/(2)}^(2)`

`(9)/(4)[\tex]</p><p></p><p>We apply it to the function:</p><p></p><p>[tex]f(x)=-1({x}^(2)+3x-6+ \boldsymbol{(9)/(4)}- \boldsymbol{(9)/(4)})`

Let's accommodate terms to make it easier:

`f(x)=-1(\underline{{x}^(2)+3x+(9)/(4)}-6-(9)/(4)`

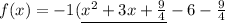
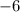`-6` Can be written as
`-(24)/(4)`:

`f(x)=-1(\underline{{x}^(2)+3x+(9)/(4)}-(24)/(4)-(9)/(4)`

`f(x)=-1(\underline{{x}^(2)+3x+(9)/(4)}-(33)/(4)`

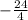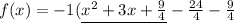
Now, what is underlined is our perfect square trinomial, let us recall its form:

`\boxed{{a}^(2)+2ab+{b}^(2)}`

Applying the same principle we are left:

`f(x)=-1[{(x+(3)/(2))}^(2)-(33)/(4))`

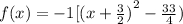
Applying distributive property we get:

`\boxed{\boxed{\boxed{f(x)=-{(x+(3)/(2))}^(2)+(33)/(4)}}}`

Therefore it will have its vertex in:
`(-1.5,\:8.25)`

The axis of symmetry is a straight line that makes the function to be projected being
`2`, for this you need some reference point, for the parabola you need the coordinate in
`x` of the vertex.

For which the axis of symmetry is
`-1.5`.

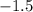I love you so much !