Answer:
Volume of smaller canister = 763.02
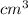
Surface area of smaller canister = 466.29

Volume of larger canister = 6104.16
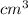
Surface area of larger canister = 1865.16

Volume becomes 8 times by doubling the size and surface area becomes 4 times by doubling the size.
Explanation:
Given that :
Diameter of Smaller canister = 9 cm
Height of Smaller canister = 12 cm
Larger canister is double the size of smaller one i.e. height and diameter are doubled.
To find:
Volume and surface area of each canister and their comparison.
Solution:
First of all, let us have a look at the formula of volume and surface area of a cylinder.
Volume,
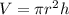
Surface Area,
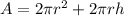
where r and h are the radius and height of the cylinder respectively.
Radius is half of diameter.
Radius of smaller canister is given by:
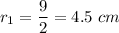
Height,
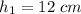
Volume,
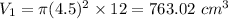
Surface Area,
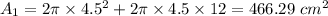
Now, Diameter / Radius and height of larger canister are doubled of smaller one.
Radius of larger canister is given by:
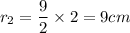
Height,
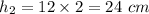
Volume,
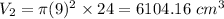
Surface Area,

Comparing the results, we can easily see that:
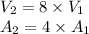
i.e. Volume becomes 8 times by doubling the size and surface area becomes 4 times by doubling the size.