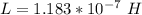Answer:
a
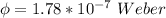
b
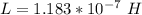
Step-by-step explanation:
From the question we are told that
The radius is

The current it carries is
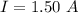
The magnetic flux of the coil is mathematically represented as
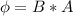
Where B is the magnetic field which is mathematically represented as
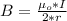
Where
 is the magnetic field with a constant value
is the magnetic field with a constant value
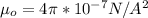
substituting value
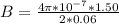

The area A is mathematically evaluated as
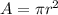
substituting values
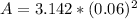
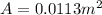
the magnetic flux is mathematically evaluated as
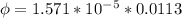
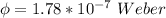
The self-inductance is evaluated as
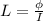
substituting values