Question

In a local ice sculpture contest, one group sculpted a block into a rectangular based pyramid. The dimensions of the base were 3 m by 5 m, and the pyramid was 3.6 m high. Calculate the amount of ice needed for this sculpture. A conical-shaped umbrella has a radius of 0.4 m and a height of 0.45 m. Calculate the amount of fabric needed to manufacture this umbrella. (Hint: an umbrella will have no base) A cone has a volume of 150 cm3 and a base with an area of 12 cm2. What is the height of the cone? Find the dimensions of a deck which will have railings on only three sides. There is 28 m of railing available and the deck must be as large as possible. A winter recreational rental company is fencing in a new storage area. They have two options. They can set it up at the back corner of the property and fence it in on four sides. Or, they can attach it to the back of their building and fence it in on three sides. The rental company has decided that the storage area needs to be 100 m2 if it is in the back corner or 98 m2 if it is attached to the back of the building. Determine the optimal design for each situation.

Answer 1

1. The amount of ice needed = 18 m²

2. The amount of fabric needed to manufacture the umbrella is 0.76 m²

3. The height of the cone, is 3.75 cm

4. The dimensions of the deck are;

Width = 28/3 m, breadth = 28/3 m

The area be 87.11 m²

5. The dimensions of the optimal design for setting the storage area at the corner, we have;

Width = 10m

Breadth = 10 m

The dimensions of the optimal design for setting the storage area at the back of their building are;

Width = 7·√2 m

Breadth = 7·√2 m

Explanation:

1. The amount of ice needed is given by the volume, V, of the pyramid given by V = 1/3 × Base area × Height

The base area = Base width × Base breadth = 3 × 5 = 15 m²

The pyramid height = 3.6 m

The volume of the pyramid = 1/3*15*3.6 = 18 m²

The amount of ice needed = 18 m²

2. The surface area of the umbrella = The surface area of a cone (without the base)

The surface area of a cone (without the base) = π×r×l

Where:

r = The radius of the cone = 0.4 m

l = The slant height = √(h² + r²)

h = The height of the cone = 0.45 m

l = √(0.45² + 0.4²) = 0.6021 m

The surface area = π×0.4×0.6021 = 0.76 m²

The surface area of a cone (without the base) = 0.76 m²

The surface area of the umbrella = 0.76 m²

The amount of fabric needed to manufacture the umbrella = The surface area of the umbrella = 0.76 m²

3. The volume, V, of the cone = 1/3×Base area, A, ×Height, h

The volume of the cone V = 150 cm³

The base area of the cone A = 120 cm²

Therefore we have;

V = 1/3×A×h

The height of the cone, h = 3×V/A = 3*150/120 = 3.75 cm

4. Given that the deck will have railings on three sides, we have;

Maximum dimension = The dimension of a square as it is the product of two equal maximum obtainable numbers

Therefore, since the deck will have only three sides, we have that the length of each side are equal and the fourth side can accommodate any dimension of the other sides giving the maximum dimension of each side as 28/3

The dimensions of the deck are width = 28/3 m, breadth = 28/3 m

The area will then be 28/3×28/3 = 784/9 =
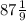`87(1)/(9)` =87.11 m²

5. The optimal design for setting the storage area at the corner of their property with four sides is having the dimensions to be that of of a square with equal sides of 10 m each as follows;

Width = 10m

Breadth = 10 m

The optimal design to have the storage area at the back of their building having a fence on only three sides, is given as follows;

Storage area specified = 98 m²

For optimal use of fencing, we have optimal side size of fencing = s = Side length of a square

s² = 98 m²

Therefore, s = √98 = 7·√2 m

Which gives the width = 7·√2 m and the breadth = 7·√2 m.