Answer:
The ratio of the volume of the larger sphere to the volume of the smaller sphere is
2352637 : 1
Explanation:
Volume of a sphere is
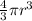
Where r is the radius
radius = diameter / 2
For First sphere
diameter = 8yards
radius = 8 / 2 = 4 yards
Volume of first sphere is
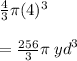
For second sphere
diameter = 1064 yards
radius = 1064 / 2 = 532 yards
Volume of second sphere is
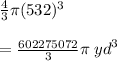
Since the volume of the second sphere is the largest
Ratio of the second sphere to the first one is
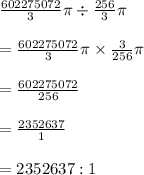
Hope this helps you