Question

The mean amount spent by a family of four on food per month is $500 with a standard deviation of $75. Assuming that the food costs are normally distributed, what is the probability that a family spends less than $410 per month?

Answer 1

The probability that a family spends less than $410 per month

P( X < 410) = 0.1151

Explanation:

Step(i):-

Given mean of the population = 500

Given standard deviation of the Population = 75

Let 'X' be the variable in normal distribution

`Z = (x-mean)/(S.D)`

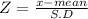
Given X = $410

`Z = (410-500)/(75) = - 1.2`

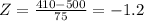
Step(ii):-

The probability that a family spends less than $410 per month

P( X < 410) = P( Z < - 1.2 )

= 0.5 - A( -1.2)

= 0.5 - A(1.2)

= 0.5 - 0.3849 ( ∵from normal table)

= 0.1151

Final answer:-

The probability that a family spends less than $410 per month

P( X < 410) = 0.1151