Question

2. Compare the function ƒ(x) = –x^2 + 4x – 5 and the function g(x), whose graph is shown. Which function has a greater absolute maximum (vertex)?

Answer 1

Explanation:

g(x) i think

Answer 2

g(x)

Explanation:

The vertex of g(x) as shwon in the graph is located in the point wich coordinates are (3.5,6.25) approximatively

We need to khow the coordinates of f(x) vertex

• Here is a way without derivating:

f(x) = -x² + 4x -5

let a be the leading factor, b the factor of x and c the constant:

• a= -1
• b= 4
• c= -5

The coordinates of a vertex are: (
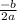`(-b)/(2a)` , f(
`(-b)/(2a)`) )

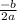-b/2a = -4/ (-1*2) = 4/2 = 2

f(2)= -2²+4*2-4 = -4+4-4 = -4

obviosly f(x) has a minimum wich less than g(x)'s maximum