Question

4. A local orchard packages apples in bags. When full, the bags weigh 5 pounds

each and contain a whole number of apples. The weights are normally distributed
with a mean of 5 pounds and a standard deviation of 0.25 pound. An inspector
weighs each bag and rejects all bags that weigh less than 4.75 pounds. What
percentage of bags will the inspector reject? *
Your answer

Answer 1

Answer: The percentage of bags will the inspector reject = 15.87%

Explanation:

Given, The weights of apple bags are normally distributed with a mean of 5 pounds and a standard deviation of 0.25 pound.

i.e.
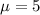`\mu=5` and
`\sigma=0.25`

Let X be the weight of any random apple bag.

Since an inspector weighs each bag and rejects all bags that weigh less than 4.75 pounds.

Then, the probability of bags will be rejected = probability that bags weigh less than 4.75 pounds.

`=P(X<4.75)\\\\=P((X-\mu)/(\sigma)<(4.75-5)/(0.25))\\\\=P(z<-1)\ \ \ [z=(X-\mu)/(\sigma)]`

`=1-P(z<1)\\\\=1-0.8413\ \ \ [\text{By z-value table}]\\\\=0.1587=15.87\%`

Hence, the percentage of bags will the inspector reject = 15.87%