Question

An entertainment services provider on the internet has 10000 subscribers paying $15 per month. It can get 1000 more subscribers for each $1 decrease in the monthly fee. Determine the monthly fee that will yield the maximum monthly revenue and the value of that revenue

Answer 1

Monthly fee is $12.5

Value of revenue is $156,250

Answer 2

Monthly fee that will yield the maximum monthly revenue is $12.5

Then the value of the maximum monthly revenue is $156 250

Explanation:

x - value of decrease

1000x - number of new subscribers for $x decrease

10000+1000x - number of subscribers after $x decrease in the monthly fee

15-1x the monthly fee after $x decrease

f(x) = (10000 + 1000x)(15 - x) ← quadratic function

For quadratic function given in standard form: f(x) =a(x-h)²+k where a<0 the f(x)=k is the maximum value of function, and occurs for x=h

`h=(-b)/(2a)\ ,\quad k=f(h)`

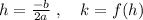
Expressing given function to standard form:

f(x) = 1000(10 + x)(15 - x)

f(x) = 1000(150 - 10x + 15x - x²)

f(x) = 1000(-x² + 5x + 150)

f(x) = -1000x² + 5000x + 150000 {a=-1000<0}

`h=(-5000)/(2\cdot(-1000))=(5000)/(2000)=\frac52=2.5\\\\k=f(2.5)=1000(10+2.5)(15-2.5)=1000\cdot12.5\cdot12.5=156\,250`

15-2.5 = 12.5