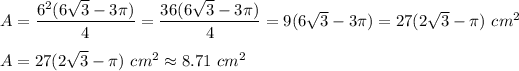Question

I REALLY NEED HELP FOR THIS ONE

Answer 1

A = 27(2√3-π) cm² ≈ 8.71 cm²

Explanation:

Area of shaded region it is area of hexagon minus area of circle.

A regular hexagon is comprised of six equilateral triangles (of the same sides).

So its area:
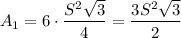`A_1=6\cdot(S^2\sqrt3)/(4)=\frac{3S^2\sqrt3}2` {S = side of the triangle}

Height (H) of such a triangle is equal to radius (R) of a circle inscribed in the hexagon:

`R = H = (S\sqrt3)/(2)`

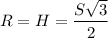
Area of shaded region:

`A=A_1-A_\circ=\frac{3S^2\sqrt3}2-\pi R^2=\frac{6S^2\sqrt3}4-\pi\left(\frac{S\sqrt3}2\right)^2=\frac{S^2(6\sqrt3-3\pi)}4`

S = 6 cm

so:

`A=\frac{6^2(6\sqrt3-3\pi)}4=\frac{36(6\sqrt3-3\pi)}4=9(6\sqrt3-3\pi)=27(2\sqrt3-\pi)\ cm^2\\\\A=27(2\sqrt3-\pi)\ cm^2\approx8.71\ cm^2`