Question

PLEASE HELP ASAP!! Write a polynomial f(x) that satisfies the following conditions. Polynomial of lowest degree with zeros of -4 (multiplicity of 1), 2 (multiplicity of 3), and with f(0)=64

Answer 1

See below.

Explanation:

So, we have the zeros -4 with a multiplicity of 1, zeros 2 with a multiplicity of 3, and f(0)=64.

Recall that if something is a zero, then the equation must contain (x - n), where n is that something. In other words, for a polynomial with a zero of -4 with a multiplicity of 1, then (x+4)^1 must be a factor.

Therefore, (x-2)^3 (multiplicity of 3) must also be a factor.

Lastly, f(0)=64 tells that when x=0, f(x)=64. Don't simply add 64 (like what I did, horribly wrong). Instead, to keep the zeros constant, we need to multiply like this:

In other words, we will have:

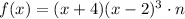`f(x)=(x+4)(x-2)^3\cdot n`, where n is some value.

Let's determine n first. We know that f(0)=64, thus:

`f(0)=64=4(-2)^3\cdot n`

`64=-32n, n=-2`

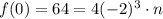
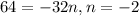
Now, let's expand:

Expand:

`f(x)=(x+4)(x^2-4x+4)(x-2)(-2)`

`f(x)=(x^2+2x-8)(x^2-4x+4)(-2)`

`f(x)=(x^4-4x^3+4x^2+2x^3-8x^2+8x-8x^2+32x-32)(-2)`

`f(x)=-2x^4+4x^3+24x^2-80x+64`

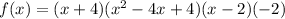
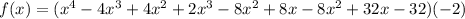
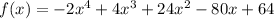
This is the simplest it can get.