Question

The standard deviations of four data sets are shown in the table below. Which

of the data sets is the most spread out?

Answer 1

Hey there! The correct answer is A. Data set C.

---

What is standard deviation?

Standard deviation is simply defined as the spread of a data set in relation to the mean of the data set. The standard deviation can be calculated with a formula as shown below.

`\displaystyle \sigma = \sqrt{(\Sigma(x_i-\mu)^2)/(N)`

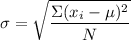
What does each variable stand for?

Each variable has a significant meaning for this formula.

• 
  `\sigma` - the standard deviation of the population
• 
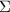  `\Sigma` - the summation of all values after the symbol
• 
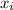  `x_i` - all data values in the set
• 
  `\mu` - the mean of the population
• 
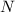  `N` - the number of data values

With this information, we can find the standard deviation of a data set.

What does standard deviation mean for a data set?

Generally speaking, statisticians want a standard deviation that is on the lower end so that conclusions can be drawn about the data that was observed.

If a standard deviation is large, that means that most of the data is quite far from the mean and the data usually disproves a hypothesis. This is undesirable since the original hypothesis cannot be proven with this experiment.

When the standard deviation is quite low, this points to data that can be relied upon since it fulfills the initial requirement to prove the hypothesis.

Therefore, since the highest standard deviation correlates with the most spread out data, A. Data set C is the answer.

Answer 2

You are correct. The higher the standard deviation is, the more spread out the data set will be. Nice work.