Question

What is the average rate of change for this function for the interval from x=3 to x=5?

(Table in attached pic)

Answer 1

a

Explanation:

i took the test

Answer 2

A. 49

Explanation:

The average rate of change for the interval ranging from x = 3 to x = 5 for the given function represented in the table above can be calculated using:

`Average rate of change = (f(x2) - f(x1))/(x2 - x1)`

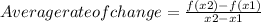
x2 = 5

x1 = 3

f(x2) = f(5) = 125

f(x1) = f(3) = 27

Thus,

`Average rate of change = (125 - 27)/(5 - 3)`

`= (98)/(2)`

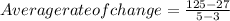
Average rate of change = 49

Average rate of change of the given table values representing an exponential function is A. 49.