Question

In a study of the decomposition of the compound XX via the reaction

X(g)⇌Y(g)+Z(g)X(g)⇌Y(g)+Z(g)

the following concentration-time data were collected:

Time (min)(min) [X](M)[X](M)
0 0.467
1 0.267
2 0.187
3 0.144
4 0.117
5 0.099
6 0.085
7 0.075

Given that the rate constant for the decomposition of hypothetical compound XX is is 1.60 M^−1⋅min^−1. Calculate the concentration of XX after 18.0 minmin .

Answer 1

Using the second-order integrated rate law to calculate the concentration of XX at 18 minutes is not possible without the initial concentration or additional data to establish a relationship between time and concentration.

Step-by-step explanation:

To calculate the concentration of compound XX after 18 minutes given a rate constant of 1.60 M−&min−&min−1, we need to apply the integrated rate law for a second-order reaction because it is given that the reaction is second-order. The second-order integrated rate law is expressed as:

1/[A] = kt + 1/[A]0

where [A] is the concentration of XX at time t, k is the rate constant, and [A]0 is the initial concentration of XX. In this case, the initial concentration is not given for the time of 18 minutes, and the values provided are insufficient to extrapolate or calculate the concentration at 18 minutes. Therefore, we are unable to solve the problem with the given data alone.

Answer 2

( About ) 0.03232 M

Step-by-step explanation:

Based on the units for this reaction it should be a second order reaction, and hence you would apply the integrated rate law equation "1 / [X] = kt + 1 / [
`X_o`]"

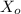This formula would be true for the following information -

{
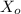`X_o` = the initial concentration of X, k = rate constant, [ X ] = the concentration after a certain time ( which is what you need to determine ), and t = time in minutes }

________

Therefore, all we have left to do is plug in the known values. The initial concentration of X is 0.467 at a time of 0 minutes, as you can tell from the given data. This is not relevant to the time needed in the formula, as we need to calculate the concentration of X after 18 minutes ( time = 18 minutes ). And of course k, the rate constant = 1.6

1 / [X] = ( 1.6 )( 18 minutes ) + 1 / ( 0.467 ) - Now let's solve for X

1 / [X] = 28.8 + 1 / ( 0.467 ),

1 / [X] = 28.8 + 2.1413...,

1 / [X] = 31,

[X] = 1 / 31 = ( About ) 0.03232 M

Now for this last bit here you probably are wondering why 1 / 31 is not 0.03232, rather 0.032258... Well, I did approximate one of the numbers along the way ( 2.1413... ) and took the precise value into account on my own and solved a bit more accurately. So that is your solution! The concentration of X after 18 minutes is about 0.03232 M