Answer:
6.28
Explanation:
The length of arc which subtends an angle
 at the center of a circle is given by
at the center of a circle is given by
 where r is the radius of circle.
where r is the radius of circle.
______________________________
given
the central angle of arc is 120°
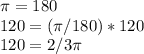
we will use value of
 as 3.14
as 3.14
r = 3
Length of this arc is
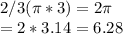
The length of the arc to the nearest hundredth of unit is 6.28