Question

Solve this problem, which steps would you take? Include any theorems, definitions, or reasons that explain the steps. Make sure you include all steps needed to solve for ∠A

Answer 1

∠A=123°.

Explanation:

From the given figure it is clear the CD and CE are two tangent lines on circle with center A.

Radius is perpendicular to the tangent at the point of tangency.

`\angle ADC=90^(\circ)`

`\angle AEC=90^(\circ)`

Smaller arc DE = (5x-2)°

It means central angle DAE is (5x-2)°.

`\angle DAE=(5x-2)^(\circ)`

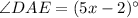
Now, ADCE is a quadrilateral and sum of all angles of a quadrilateral is 360 degrees.

`\angle ADC+\angle DCE+\angle AEC+\angle DAE=360^(\circ)`

`90^(\circ)+(2x+7)^(\circ)+90^(\circ)+(5x-2)^(\circ)=360^(\circ)`

`(7x+5)^(\circ)+180^(\circ)=360^(\circ)`

`(7x+5)^(\circ)=360^(\circ)-180^(\circ)`

`(7x+5)^(\circ)=180^(\circ)`

`7x+5=180`

`7x=175`

`x=25`

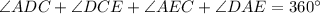
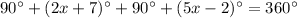
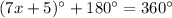
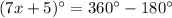
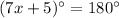
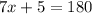
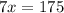
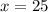
The value of x is 25.

`\angle A=5x-2=5(25)-2=125-2=123^(\circ)`

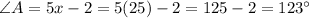
Therefore, the measure of ∠A is 123°.