Question

Which of the following integrals will determine the volume of the solid generated by revolving the region bounded by the curves y = 6x, y = x and y = 24 about the y-axis using the shell method?

a) integral^24_0 2 pi x(24 - 5x) dx
b) integral^24_0 5/3 pi y^2 dy
c) integral^4_0 10 pi x^2 dx + integral^24_4 2 pi x(24 - x) dx integral^4_0 25 pi x^2 dx + integral^24_4 2 pi x(24 - x) dx
d) integral^4_0 25 pi x^2 dx + integral^24_4 pi (24 - x)^2 dx
e) integral^24_0 25 pi y^2/36 dy

Answer 1

The answer is "Option C."

Explanation:

`y=6x, \ \ y=x, \ \ , y=24,\\`

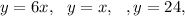
In this we calculate two points that are (0,4) and(4,24)

on[0,4]

shell radius=x

height = 6x-x

=5x

on[4,24]

shell radius=x

height = 24x-x

6x=24

x=4

Calculating shell volume by shell method:

`v=\int\limits^b_a {2\pi(radius) \cdot(height)} \, dx \\`

`=\int\limits^4_0 {2\pi(x) \cdot(5x)} \, dx +\int\limits^(24)_4 {2\pi(x) \cdot(24-x)} \, dx \\\\=\int\limits^4_0 {10\pi(x^2) dx +\int\limits^(24)_4 {2\pi x(24-x)} \, dx`

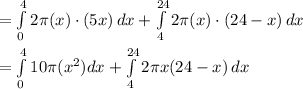
That's why the answer is "Option C".