Answer:
Following are the answer to this question:
Step-by-step explanation:
In option 1:
The value of n is= 7, which is (base case)
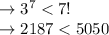
when n=k for the true condition:
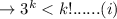
when n=k+1 it tests the value:
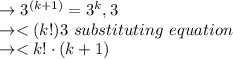
since k>6 hence the value is KH>3 hence proved.
In option 2:
when:
for n=1:(base case)
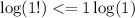
0<=0 \\ condition is true
when the above statement holds value n=1
when n=k
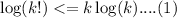
when n=k+1
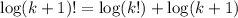
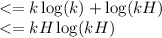
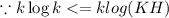
![[\therefore KH>K \Rightarrow \log(KH>\loK)]](https://img.qammunity.org/2021/formulas/computers-and-technology/college/b4m8f5guqk1y2p6momfa0wk1rbjkos54om.png)
In option 3:
when n=1:
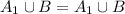
when n=k
![\to (A_1\cap A_2 \cap.....A_k) \cup B\\=(A_1\cup B) \cap(A_2\cup B_2)....(A_k \capB).....(a)\\\to n= k+1\\ \to (A_1\cap A_2 \cap.....A_(kH)) \cup B= (A_1\cup B)\\\\\to [(A_1\cap A_2 \cap.....A_(k)) \cup B]\cap (A_(KH)\cup B)\\\\\to [(A_1\cup B) \cap (A_2 \cup B) \cap (A_3\cup B).....(A_k\cup B)\cap (A_(k+1) \cup B)\\\\ \ \ \ \ \ \ substituting \ equation \ a \\\\](https://img.qammunity.org/2021/formulas/computers-and-technology/college/bj4qbd1mjz6tp90qnj0rf0rouoifrgvdy9.png)
hence n=k+1 is true.