Question

Verify by direct substitution that the given power series is a solution of the indicated differential equation. [Hint: For a power x2n + 1 let k = n + 1.] y = (-1) nx2n, (1 + x2)y' + 2xy = 0

Answer 1

The given power series
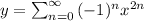`y =\sum^(\infty)_(n=0) {(-1)^n x^(2n)}` is a solution of the differential equation (1+x^2)y' + 2xy = 0

Explanation:

This is a very trivial exercise, follow the steps below for the solution:

Step 1: Since n = 0, 1, 2, 3, 4, ........, Substitute the values of n into equation (1) below.

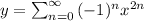`y =\sum^(\infty)_(n=0) {(-1)^n x^(2n)}`.....................(1)

`y = 1 - x^2 + x^4 - x^6 + x^8.........`

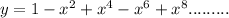
Step 2: Find the derivative of y, i.e. y'

`y' = -2x + 4x^3 - 6x^5 + 8x^7 .............`

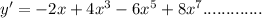
Step 3: Substitute y and y' into equation (2) below:

`(1+x^2)y' + 2xy = 0\\\\(1+x^2)(-2x + 4x^3 - 6x^5 + 8x^7......) + 2x(1 - x^2 + x^4 - x^6 + x^8.......) = 0\\\\-2x+ 4x^3 - 6x^5 + 8x^7........ - 2x^3 +4x^5 - 6x^7 + 8x^9 ......+ 2x - 2x^3 + 2x^5 - 2x^7 + 2x^9...... = 0\\\\0 = 0`

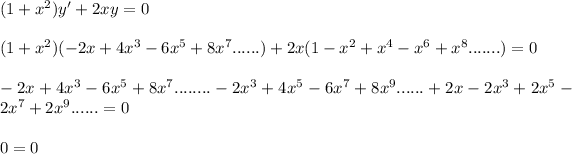
(Verified)

Since the LHS = RHS = 0, the given power series
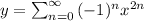`y =\sum^(\infty)_(n=0) {(-1)^n x^(2n)}` is a solution of the differential equation (1+x^2)y' + 2xy = 0