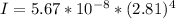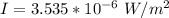Question

Use Stefan's law to find the intensity of the cosmic background radiation emitted by the fireball of the Big Bang at a temperature of 2.81 K.

Answer 1

Complete Question

Use Stefan's law to find the intensity of the cosmic background radiation emitted by the fireball of the Big Bang at a temperature of 2.81 K. Remember that Stefan's Law gives the Power (Watts) and Intensity is Power per unit Area (W/m2).

Answer:

The intensity is
`I = 3.535 *10^(-6) \ W/m^2`

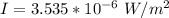
Step-by-step explanation:

From the question we are told that

The temperature is
`T = 2.81 \ K`

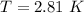
Now According to Stefan's law

`Power(P) = \sigma * A * T^4`

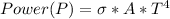
Where
`\sigma` is the Stefan Boltzmann constant with value
`\sigma = 5.67*10^(-8) m^2 \cdot kg \cdot s^(-2) K^(-1)`

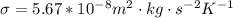
Now the intensity of the cosmic background radiation emitted according to the unit from the question is mathematically evaluated as

`I = (P)/(A)`

=>
`I = (\sigma * A * T^4)/(A)`

=>
`I = \sigma * T^4`

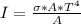
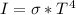
substituting values

`I = 5.67 *10^(-8) * (2.81)^4`

`I = 3.535 *10^(-6) \ W/m^2`