Answer: 200
=====================================
Work Shown:
One approach is to simplify the stuff under the second power exponent. After that simplification, you would then square the result.
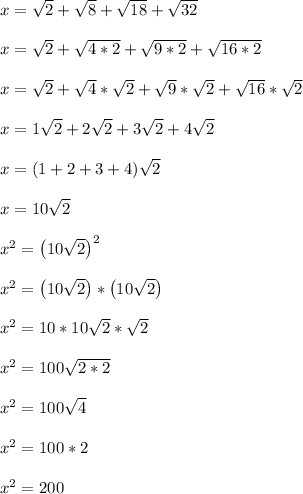
So,
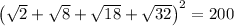
-----------------------------------------------------
Checking the answer:
Using a calculator,
sqrt(2)+sqrt(8)+sqrt(18)+sqrt(32) = 14.142135623731
Then you square that to get (14.142135623731)^2 = 200.000000000001
Your calculator may not have that 1 at the end. It shouldn't be there and it's a result of rounding error. But it's close enough to 200.