Question

PLEASE HELP the formula m=12,000+12,000rt/12t gives keri's monthly loan payment where t is the annual interest rate and t is the length of the loan, in years. Keri decideds that she can afoord at most a $275

Answer 1

Here's the keywords you need! :)

example of an interest rate and a loan length that costs under $275/month (example: 4-year loan at 2% interest)

monthly payment for the loan you described (example: 4-year loan at 2% interest is $270/month)

statement that the monthly payment for the loan you described is less than or equal to $275 (example: $270/month payment is less than $275)

Just got it right on edge 2020, hope this helps!! :)

Answer 2

The answer is below

Explanation:

The formula m = (12,000 + 12,000rt)/12t gives Keri's monthly loan payment, where r is the annual interest rate and t is the length of the loan, in years. Keri decides that she can afford, at most, a $275 monthly car payment. Give an example of an interest rate greater than 0% and a loan length that would result in a car payment Keri could afford. Provide support for your answer.

Answer: Let us assume an annual interest rate (r) = 10% = 0.1. The maximum monthly payment (m) Keri can afford is $275. i.e. m ≤ $275. Using the monthly loan payment formula, we can calculate a loan length that would result in a car payment Keri could afford.

`m=(12000+12000rt)/(12t)\\ but\ m\leq275, \ and \ r=10\%=0.1\\275= (12000+12000(0.1)t)/(12t)\\275= (12000)/(12t) +(12000(0.1))/(12t)\\275= (1000)/(t) + 100\\275-100= (1000)/(t) \\175= (1000)/(t) \\175t = 1000\\t= (1000)/(175)\\ t=5.72\ years`

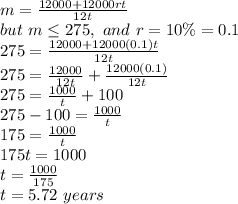
The loan must be at least for 5.72 years for an annual interest rate (r) of 10%