Answer:
a) The first arrow reaches a maximum height of 56.712 meters, whereas second arrow reaches a maximum height of 342.816 meters, b) Both arrows have a total mechanical energy at their maximum height of 201.720 joules.
Step-by-step explanation:
a) The first arrow is launch in a parabolic way, that is, horizontal speed remains constant and vertical speed changes due to the effects of gravity. On the other hand, the second is launched vertically, which means that velocity is totally influenced by gravity. Let choose the ground as the reference height for each arrow. Each arrow can be modelled as particles and by means of the Principle of Energy Conservation:
First arrow
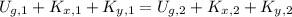
Where:
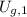 ,
,
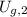 - Initial and final gravitational potential energy, measured in joules.
- Initial and final gravitational potential energy, measured in joules.
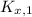 ,
,
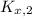 - Initial and final horizontal translational kinetic energy, measured in joules.
- Initial and final horizontal translational kinetic energy, measured in joules.
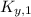 ,
,
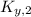 - Initial and final vertical translational kinetic energy, measured in joules.
- Initial and final vertical translational kinetic energy, measured in joules.
Now, the system is expanded and simplified:
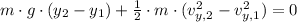
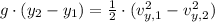
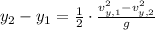
Where:
 .
.
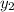 - Initial and final height of the arrow, measured in meters.
- Initial and final height of the arrow, measured in meters.
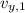 ,
,
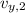 - Initial and final vertical speed of the arrow, measured in meters.
- Initial and final vertical speed of the arrow, measured in meters.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
The initial vertical speed of the arrow is:
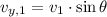
Where:
 - Magnitude of the initial velocity, measured in meters per second.
- Magnitude of the initial velocity, measured in meters per second.
 - Initial angle, measured in sexagesimal degrees.
- Initial angle, measured in sexagesimal degrees.
If
 and
and
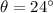 , the initial vertical speed is:
, the initial vertical speed is:
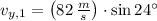
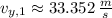
If
 ,
,
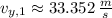 and
and
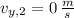 , the maximum height of the first arrow is:
, the maximum height of the first arrow is:
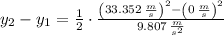
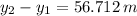
Second arrow
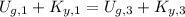
Where:
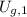 ,
,
 - Initial and final gravitational potential energy, measured in joules.
- Initial and final gravitational potential energy, measured in joules.
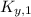 ,
,
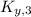 - Initial and final vertical translational kinetic energy, measured in joules.
- Initial and final vertical translational kinetic energy, measured in joules.
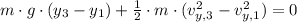

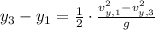
If
 ,
,
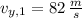 and
and
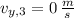 , the maximum height of the first arrow is:
, the maximum height of the first arrow is:
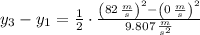
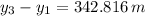
The first arrow reaches a maximum height of 56.712 meters, whereas second arrow reaches a maximum height of 342.816 meters.
b) The total energy of each system is determined hereafter:
First arrow
The total mechanical energy at maximum height is equal to the sum of the potential gravitational energy and horizontal translational kinetic energy. That is to say:
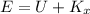
The expression is now expanded:
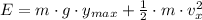
Where
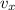 is the horizontal speed of the arrow, measured in meters per second.
is the horizontal speed of the arrow, measured in meters per second.

If
 and
and
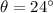 , the horizontal speed is:
, the horizontal speed is:
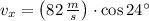
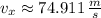
If
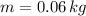 ,
,
 ,
,
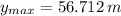 and
and
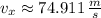 , the total mechanical energy is:
, the total mechanical energy is:
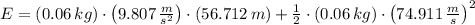

Second arrow:
The total mechanical energy is equal to the potential gravitational energy. That is:

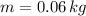 ,
,
 and
and

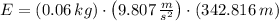

Both arrows have a total mechanical energy at their maximum height of 201.720 joules.