Answer:
a)
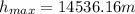
b)
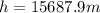
c)
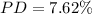 The estimate is low.
The estimate is low.
Step-by-step explanation:
a) Using the energy conservation we have:

we have kinetic energy intially and gravitational potential energy at the maximum height.
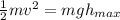
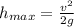
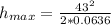
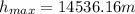
b) We can use the equation of the gravitational force
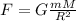 (1)
(1)
We have that:
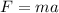 (2)
(2)
at the surface G will be:
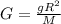
Now the equation of an object at a distance x from the surface.
is:
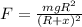
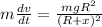
Using that dv/dt is vdx/dt and integrating in both sides we have:
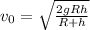

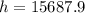
c) The difference is:
So the percent difference will be:

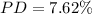
The estimate is low.
I hope it helps you!