Answer:
a
The estimate for the percentage of yellow peas lie within the confidence interval 23.66% and 30.83 %
b
Since the expected value for the estimate of the yellow peas lies between the confidence interval it means that the given estimate of yellow peas does not contradict the expectation
Explanation:
From the question we are told that
The number of green peas is
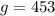
The number of yellow peas is
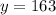
The sample size is
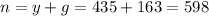
The sample proportion of the yellow peas is
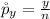
substituting values
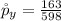
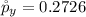
Given that the confidence level is
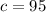 %
%
The level of significance is
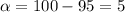 %
%
The critical values at this level of significance is obtained from the table of critical values as
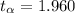
Now the confidence interval is mathematically evaluated as
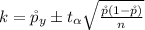
substituting values
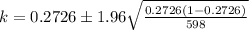
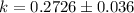
So the 95% confidence interval is
k = ( 0.2366, 0.3083)
This mean that the estimate of the yellow peas(25%) lies between
23.66% and 30.83 %
Given that the expected value for the estimate of the yellow peas lies between the confidence interval it means that the given estimate of yellow peas does not contradict the expectation