Answer:
The percent of households with rates from $100 to $115. is
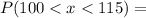 94.1%
94.1%
Explanation:
From the question we are told that
The mean rate is
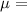 $ 106.50 per month
$ 106.50 per month
The standard deviation is
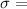 $3.85
$3.85
Let the lower rate be
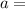 $100
$100
Let the higher rate be
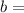 $ 115
$ 115
Assumed from the question that the data set is normally
The estimate of the percent of households with rates from $100 to $115. is mathematically represented as
![P(a < x < b) = P[ (a -\mu)/(\sigma ) } < (x- \mu)/(\sigma) < (b - \mu )/(\sigma ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/ly6y01l2r2dk0q15cwqti2ym5obe84g38v.png)
here x is a random value rate which lies between the higher rate and the lower rate so
![P(100 < x < 115) = P[ (100 -106.50)/(3.85) } < (x- \mu)/(\sigma) < (115 - 106.50 )/(3.85 ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/bx3ndyojul6jsbvjp832st8hdnvyxugjqg.png)
![P(100 < x < 115) = P[ -1.688< (x- \mu)/(\sigma) < 2.208 ]](https://img.qammunity.org/2021/formulas/mathematics/college/bm28q1bw1k24xq56p6p3rdz3kzmugci1my.png)
Where
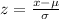
Where z is the standardized value of x
So
![P(100 < x < 115) = P[ -1.688< z < 2.208 ]](https://img.qammunity.org/2021/formulas/mathematics/college/qhh4n423645z936yirrtgmsm2dg2mdpy4d.png)
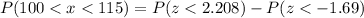
Now from the z table we obtain that
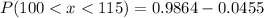
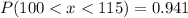
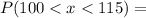 94.1%
94.1%