Question

Find all points (if any) of horizontal and vertical tangency to the curve. Use a graphing utility to confirm your results. (If an answer does not exist, enter DNE.)

x=1-t , y=t^2

Horizontal tangent
(x,y)=________
Vertical tangent
(x,y)=________

Answer 1

Horizontal tangent

(x, y) = (1, 0)

Vertical tangent

(x, y) = DNE

Explanation:

The equation for the slope (m) of the tangent line at any point of a parametric curve is:

`m = ((dy)/(dt) )/((dx)/(dt) )`

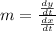
Where
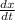`(dx)/(dt)` and
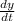`(dy)/(dt)` are the first derivatives of the horizontal and vertical components of the parametric curves. Now, the first derivatives are now obtained:

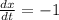`(dx)/(dt) = -1` and
`(dy)/(dt) = 2\cdot t`

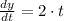
The equation of the slope is:

`m = -2\cdot t`

As resulting expression is a linear function, there are no discontinuities and for that reason there are no vertical tangents. However, there is one horizontal tangent, which is:

`-2\cdot t = 0`

`t = 0`

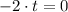
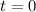
The point associated with the horizontal tangent is:

`x = 1 - 0`

`x = 1`

`y = 0^(2)`

`y = 0`

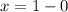
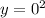
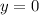
The answer is:

Horizontal tangent

(x, y) = (1, 0)

Vertical tangent

(x, y) = DNE