Question

The life in hours of a battery is known to be normally distributed, with a standard deviation of 1.25 hours. A random sample of 10 batteries has a mean life x = 40.5 hours.

a) Is there evidence to support the claim that battery life exceeds 40 hours? Use
α = 0.05.
b) What is the P-value for this test?

Answer 1

a) Test statistic

Z = 1.265 < 1.96 at 0.05 level of significance

The battery life is not exceeds 40 hours

b)

p- value = 0.8962

Explanation:

Step(i):-

Given sample size 'n' =10

Mean of the sample x⁻ = 40.5 hours

Mean of of the Population μ = 40 hours

Standard deviation of the Population = 1.25 hours

Step(ii):-

Null Hypothesis:H₀: μ = 40 hours

Alternative Hypothesis :H₁ : μ < 40 hours

step(ii):-

Test statistic

`Z = (x^(-) -mean)/((S.D)/(√(n) ) )`

`Z = (40.5 -40)/((1.25)/(√(10) ) )`

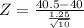
Z = 1.265

Level of significance = 0.05

Z₀.₀₅ = 1.96

Z = 1.265 < 1.96 at 0.05 level of significance

The battery life is not exceeds 40 hours

Step(iii):-

P - value

P( Z < 1.265) = 0.5 + A( 1.265)

= 0.5 + 0.3962

= 0.8962

P( Z < 1.265) = 0.8962

i ) p- value = 0.8962 > 0.05

Accept H₀

There is no significant

The battery life is not exceeds 40 hours