Answer:
(a) P(X=3) = 0.093
(b) P(X≤3) = 0.966
(c) P(X≥4) = 0.034
(d) P(1≤X≤3) = 0.688
(e) The probability that none of the 25 boards is defective is 0.277.
(f) The expected value and standard deviation of X is 1.25 and 1.089 respectively.
Explanation:
We are given that when circuit boards used in the manufacture of compact disc players are tested, the long-run percentage of defectives is 5%.
Let X = the number of defective boards in a random sample of size, n = 25
So, X ∼ Bin(25,0.05)
The probability distribution for the binomial distribution is given by;

where, n = number of trials (samples) taken = 25
r = number of success
p = probability of success which in our question is percentage
of defectivs, i.e. 5%
(a) P(X = 3) =
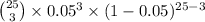
=
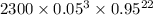
= 0.093
(b) P(X
 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
=
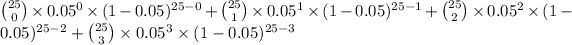
=
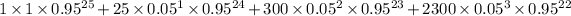
= 0.966
(c) P(X
 4) = 1 - P(X < 4) = 1 - P(X
4) = 1 - P(X < 4) = 1 - P(X
 3)
3)
= 1 - 0.966
= 0.034
(d) P(1 ≤ X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3)
=
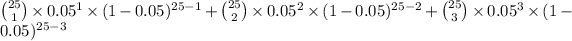
=
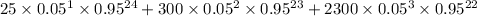
= 0.688
(e) The probability that none of the 25 boards is defective is given by = P(X = 0)
P(X = 0) =
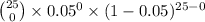
=

= 0.277
(f) The expected value of X is given by;
E(X) =
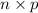
=
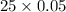 = 1.25
= 1.25
The standard deviation of X is given by;
S.D.(X) =
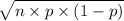
=
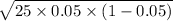
= 1.089