Question

An angle measures 54° more than the measure of its supplementary angle. What is the measure of each angle?

Answer 1

Explanation:

we know that If two angles are complementary, then their sum is equal to 90 degrees

Letx -----> the measure of an angle

y-----> the measure of he other angle

we know thatx+y=90 -----> y=90

-x -----> equation

Ax=y+54 ----> equation

Bsubstitute equation B in equation A and solve for yy=90-(y+54)

y=90-y-542y=36y=18°

Find the value of xx=y+54 -----> x=18+54=72°

thereforeThe measure of the angles are 72 degrees and 18 degrees

Answer 2

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

`\blue{\textsf{\textbf{\underline{\underline{Question:-}}}}`

An angle measures 54º more than the measure of its supplementary angle. What is the measure of each angle?

`\blue{\textsf{\textbf{\underline{\underline{Answer:-}}}}`

Angle Measurements:- 63º and 117º

`\blue{\textsf{\textbf{\underline{\underline{How\:to\:Solve:-}}}}`

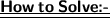
Supplementary angles add up to 180º.

Now, let the unknown angle be n.

Set up an equation:-

`\bigstar`
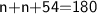`\textsf{n+n+54=180}` (remember, supplementary angles add up to 180)

Add the n's :

`\textsf{2n+54=180}`

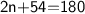
Subtract 54 on both sides:

`\textsf{2n=126}`

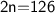
Divide by 2 on both sides:

`\textsf{n=63\textdegree}`

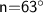
Now, add 54 to find the other angle:

63+54=117

Check:-

We can easily check our work by adding the two angles together and seeing whether or not we end up with 180º.

`\textsf{63+117=180}`

`\textsf{180=180}\LARGE\checkmark`

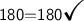
LHS=RHS (Left-Hand Side = Right-Hand Side)

Hence, the angles are 63 and 117.
`\checkmark`

Good luck.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -