Question

Please answer this ASAP. The question is down below. Thank you!

Answer 1

`y = .5x^2 -2x -5`

Explanation:

Well we can start by seeing if the parabola is the same width by comparing it to its parent function ( y = x^2 )

In y = x^2 the 2nd lowest point is just up 1 and right 1 away from the vertex.

This is not true for our parabola.

So we can widen it by to the desidered width by making the x^2 into a .5x^2.

So far we’ve got y = .5x^2

Now the parabola y intercept is at -5.

So we can add a -5 into the equation making it.

y = .5x^2 - 5

Now for the x value.

So we can find the x value by seeing how far away the parabola is from from the y axis.

So the x value is -2x.

So the full equation is
`y = .5x^2 -2x -5`

Look at the image below to compare.

Answer 2

Answer:
`Vertex: y=(1)/(2)(x-2)^2-7`

`Standard: y=(1)/(2)x^2-2x-5`

Transformations: vertical shrink by a factor of 1/2,

horizontal shift 2 units to the right,

vertical shift 7 units down.

Explanation:

Vertex form: y = a(x - h)² + k

Standard form: y = ax² + bx + c

Given: Vertex (h, k) = (2, -7), the y-intercept (0, c) = (0, -5)

Input those values into the Vertex form to solve for the a-value

-5=a(0 - 2)² - 7

2 = a(- 2)²

2 = 4a

`(1)/(2)=a`

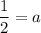
a) Input a = 1/2 and (h, k) = (2, -7) into the Vertex form

`\large\boxed{y=(1)/(2)(x-2)^2-7}`

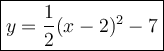
b) You can plug in a = 1/2, c = -5, (x, y) = (2, -7) to solve for "b"

or

You can expand the Vertex form (which is what I am going to do):

`y=(1)/(2)(x-2)^2-7\\\\\\y=(1)/(2)(x^2-4x+4)-7\\\\\\y=(1)/(2)x^2-2x+2-7\\\\\\\large\boxed{y=(1)/(2)x^2-2x-5}`

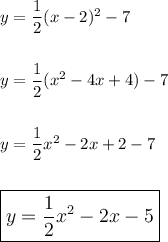
c) Use the Vertex form to describe the transformations as follows:

• a is the vertical stretch (if |a| > 1) or shrink (if |a| < 1)
• h is the horizontal shift (positive is to the right, negative is to the left)
• k is the vertical shift (positive is up, negative is down)

`y=(1)/(2)(x-2)^2-7`

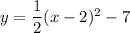
a = 1/2 --> vertical shrink by a factor of 1/2

h = 2 --> horizontal shift 2 units to the right

k = -7 --> vertical shift 7 units down