Answer:
(a) The mean weight of beer used to fill each bottle is 16 ounces.
(b) The answer of part (a) would not change.
Explanation:
A local bottler, Fossil Cove, wants to ensure that an average of 16 ounces of beer is used to fill each bottle.
Ben takes a random sample of n = 48 bottles and finds the average weight to be
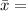 15.8 ounces. Also it is known that the standard deviation is, σ = 0.8 ounces.
15.8 ounces. Also it is known that the standard deviation is, σ = 0.8 ounces.
(a)
The hypothesis can be defined as follows:
H₀: The mean weight of beer used to fill each bottle is 16 ounces, i.e. μ = 16.
Hₐ: The mean weight of beer used to fill each bottle is not 16 ounces, i.e. μ ≠ 16.
Assume that the significance level of the test is, α = 0.05.
As the population standard deviation is provided, we will use a z-test for single mean.
Compute the test statistic value as follows:
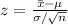

The test statistic value is -1.732.
Decision rule:
If the p-value of the test is less than the significance level then the null hypothesis will be rejected.
Compute the p-value for the two-tailed test as follows:
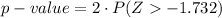
![=2* [1-P(Z<1.732)]\\\\=2* [1-0.04182]\\\\=0.08364\\\\\approx 0.084](https://img.qammunity.org/2021/formulas/mathematics/college/6m7n8pp1dz5apdg3s1v0ceb82wmtd8il51.png)
*Use a z-table for the probability.
The p-value of the test is 0.084.
p-value = 0.084 > α = 0.05
The null hypothesis will not be rejected.
Thus, it can be concluded that the mean weight of beer used to fill each bottle is 16 ounces.
(b)
The standard deviation of a random variable is the square root of the variance.
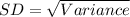
So, if the variance was 0.64, then the standard deviation will be:
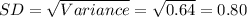
Thus, the answer of part (a) would not change.