Answer:
The Taylor series is
![$$\sum_(n=0)^(\infty) [((-1)^n)/((2n +1)!) (x)^(2n+1)]](https://img.qammunity.org/2021/formulas/mathematics/college/6lgy0pq010shqqc155elfmyzhs7tj4thxg.png)
Explanation:
From the question we are told that
The function is
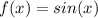
This is centered at
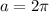
Now the next step is to represent the function sin (x) in it Maclaurin series form which is
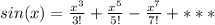
=>
![sin (x) = $$\sum_(n=0)^(\infty) [((-1)^n)/((2n +1)!) (x)^(2n+1)]](https://img.qammunity.org/2021/formulas/mathematics/college/urk8qxefz7m2itkdoagisd7ppves3pc8pb.png)
Now since the function is centered at
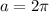
We have that
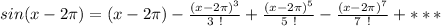
This above equation is generated because the function is not centered at the origin but at
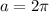
![sin (x-2 \pi ) = $$\sum_(n=0)^(\infty) [((-1)^n)/((2n +1)!) (x - 2 \pi)^(2n+1)]](https://img.qammunity.org/2021/formulas/mathematics/college/j9zt6yta80lqxvucs7l8vumhmktyt8xvu0.png)
Now due to the fact that
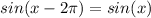
This because
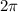 is a constant
is a constant
Then it implies that the Taylor series of the function centered at
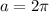 is
is
![$$\sum_(n=0)^(\infty) [((-1)^n)/((2n +1)!) (x)^(2n+1)]](https://img.qammunity.org/2021/formulas/mathematics/college/6lgy0pq010shqqc155elfmyzhs7tj4thxg.png)