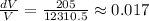Question

The circumference of a sphere was measured to be 90 cm with a possible error of 0.5 cm.

(a) Use differentials to estimate the maximum error in the calculated surface area. (Round your answer to the nearest integer.)
cm2
What is the relative error? (Round your answer to three decimal places.)
(b) Use differentials to estimate the maximum error in the calculated volume. (Round your answer to the nearest integer.)
cm^3
What is the relative error? (Round your answer to three decimal places.)

Answer 1

Error in the sphere's surface: 29
`cm^2` and relative error in surface measure: 0.011

Error in the sphere's volume: 205
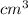`cm^3` and relative error in the volume measure: 0.017

Explanation:

(a)

The measured length (l) of the circumference is 90 cm with an error of 0.5 cm, that is:

`l=2\,\pi\,R=90\,cm\\R=(90)/(2\,\pi) \,cm=(45)/(\pi) \,cm=14.3239\,\,cm`

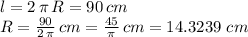
and with regards to the error:

`dl=0.5 \, cm\\dl=2\,\pi\,dR\\dR=(dl)/(2\,\pi) =(1)/(4\,\pi) cm = 0.0796\,cm`

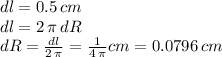
then when we use the formula for the sphere's surface, we get:

`S=4\,\pi\,R^2\\dS=4\,\pi\,2\,R\,(dR)\\dS=8\,\,\pi\.((45)/(\pi) \,\,cm)\,((1)/(4\pi)\,cm) =(90)/(\pi) \,\,cm^2\approx \,29\,cm^2`

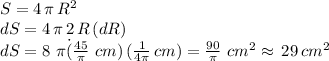
Then the relative error in the surface is:

`(dS)/(S) =(90/\pi)/(4\,\pi\,R^2) =(1)/(90) =0.011`

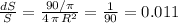
(b)

Use the formula for the volume of the sphere:

`V=(4\,\pi)/(3) R^3\\dV=(4\,\pi)/(3)\,3\,R^2\,(dR)=4\,\pi\,R^2\,((1)/(4\pi)) \,cm=((45)/(\pi))^2 \,\,cm^3\approx 205\,\,cm^3`

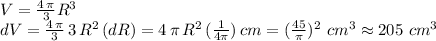
Then the relative error in the volume is:

`(dV)/(V) =(205)/(12310.5) \approx 0.017`