Question

How would I solve? Please help!

Use the quadratic formula -b + √b² - 4ac
to solve for the x-intercepts in the
following equations.
a.
0 = x²- 2x - 15
a= ? b= -?
c=?
b.
The x-intercepts of the function y = x² – 2x – 15 are ( ?,0) and -?,0) (A.K.)
c.
The x-value of the vertex, located halfway between the two x-intercepts is: _?(A.K.)
d.
After you plug in the x-value of the vertex back into the function
y = x²- 2x - 15, you get the y-value of the vertex, _? (A.K.)
e.
The vertex, written as a paired coordinate is (_?_,_?_).

​

Answer 1

• intercepts: (-3, 0), (5, 0)
• vertex: (1, -16)

Explanation:

a. Compare the given equation to the standard form to see what the coefficients are:

ax^2 +bx +c = 0

x^2 -2x -15 = 0

Comparing these, we see that ...

a = 1, b = -2, c = -15

__

b. Using the quadratic formula we find the intercepts to be ...

`x=(-b\pm√(b^2-4ac))/(2a)\\\\x=(-(-2)\pm√((-2)^2-4(1)(-15)))/(2(1))\\\\=(2\pm√(64))/(2)=1\pm4\\\\x=\{-3,5\}`

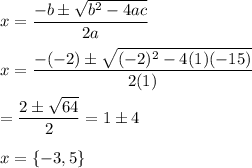
The x-intercepts of the function are (-3, 0) and (5, 0).

__

c. The midpoint between the vertices is ...

x = (-3+5)/2

x = 1

__

d. The value of the function for x=1 is ...

y = 1^2 -2(1) -15

y = -16

__

e. The coordinates of the vertex are ...

(x, y) = (1, -16)