Question

A researcher is interested in finding a 95% confidence interval for the mean number of times per day that college students text. The study included 102 students who averaged 25.7 texts per day. The standard deviation was 23.9 texts. Round answers to 3 decimal places where possible.

a. With 95% confidence the population mean number of texts per day is between _____ and ______ texts.
b. If many groups of 132 randomly selected members are studied, then a different confidence interval would be produced from each group. About _____ percent of these confidence intervals will contain the true population number of texts per day and about _____ percent will not contain the true population mean number of texts per day.

Answer 1

Complete Question

A researcher is interested in finding a 95% confidence interval for the mean number of times per day that college students text. The study included 210 students who averaged 28 texts per day. The standard deviation was 21 texts.

Round your answers to two decimal places.

A. The sampling distribution follows a [ Select ] ["F", "normal", "T", "Chi-square"] distribution.

B. With 95% confidence the population mean number of texts per day of is between [ Select ] ["24.92", "25.79", "27.37", "25.14"] and [ Select ] ["31.19", "31.20", "29.28", "30.86"] texts.

C. If many groups of 210 randomly selected students are studied, then a different confidence interval would be produced from each group. About [ Select ] ["5", "95", "1", "99"] percent of these confidence intervals will contain the true population mean number of texts per day and about [ Select ] ["95", "99", "5", "1"] percent will not contain the true population mean number of texts per day.

Answer:

a. With 95% confidence the population mean number of texts per day is between
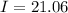`I = 21.06` and
`I = 30.33` texts.

b

If many groups of 132 randomly selected members are studied, then a different confidence interval would be produced from each group. About 95% percent of these confidence intervals will contain the true population number of texts per day and about 5% percent will not contain the true population mean number of texts per day.

Explanation:

From the question we are told that

The sample size is
`n = 102`

The population mean is
`\mu = 25.7`

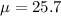
The standard deviation is
`\sigma = 23.9`

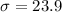
Generally the standard error of mean is mathematically evaluated as

`\sigma_e = (\sigma)/(√(n ) )`

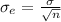
substituting values

`\sigma_e = (23.9)/(√(102 ) )`

`\sigma_e = 2.3665`

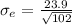
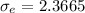
Given that the level of confidence is 95% then the level of significance will be

`\alpha = 100 -95`

`\alpha =`5%

=>
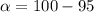
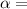`\alpha = 0.05`

Now the critical values of this level of significance is obtained from the critical value table as

`t_(n,\alpha ) = t_(102,0.05) = 1.96`

Generally the 95% confidence interval is mathematically represented as

`I = \mu \pm t_(102, 0.05) * \sigma_e`

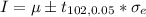
substituting values

`I = 25.7 \pm 1.96 *2.3665`

`I = 25.7 \pm 4.638`

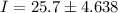
`I = 30.33` and
`I = 21.06`

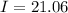
So the interval is