Question

The floor of a shed given on the right has an area of 44 square feet . The floor is in the shape of a rectangle whose length is 3 less than twice the width. Find the length and width of the floor of the shed.

Answer 1

The length and width of the floor of the shed are 8 feet and 5.5 feet, respectively.

Explanation:

Given that the shape of the shed is a rectangle, the expression for the area is:

`A = w \cdot l`

Where
`w` and
`l` are the width and length of the shed, measured in feet. In addition, the statement shows that
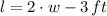`l = 2\cdot w - 3\,ft`. Then, the equation of area is expanded by replacing length:

`A = w\cdot (2\cdot w - 3)`

`A = 2\cdot w^(2) - 3\cdot w`

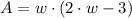
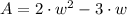
If
`A = 44\,ft^(2)`, then, a second-order polynomial is formed:

`2\cdot w^(2)-3\cdot w - 44 = 0`

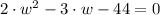
The roots of this equation are found via General Equation for Second-Order Polynomials:

`w_(1) = (11)/(2)\,ft` and
`w_(2) = -4\,ft`

Only the first roots is a physically reasonable solution. Then, the length of the shed is:

`l = 2\cdot \left((11)/(2)\,ft \right)-3\,ft`

`l = 8\,ft`

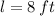
The length and width of the floor of the shed are 8 feet and 5.5 feet, respectively.