Answer:
The transformations needed to obtain the new function are horizontal scaling, vertical scaling and vertical translation. The resultant function is
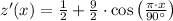 .
.
The domain of the function is all real numbers and its range is between -4 and 5.
The graph is enclosed below as attachment.
Explanation:
Let be
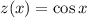 the base formula, where
the base formula, where
 is measured in sexagesimal degrees. This expression must be transformed by using the following data:
is measured in sexagesimal degrees. This expression must be transformed by using the following data:
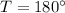 (Period)
(Period)
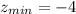 (Minimum)
(Minimum)
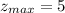 (Maximum)
(Maximum)
The cosine function is a periodic bounded function that lies between -1 and 1, that is, twice the unit amplitude, and periodicity of
 radians. In addition, the following considerations must be taken into account for transformations:
radians. In addition, the following considerations must be taken into account for transformations:
1)
 must be replaced by
must be replaced by
 . (Horizontal scaling)
. (Horizontal scaling)
2) The cosine function must be multiplied by a new amplitude (Vertical scaling), which is:
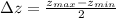
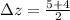
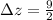
3) Midpoint value must be changed from zero to the midpoint between new minimum and maximum. (Vertical translation)
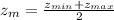
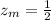
The new function is:
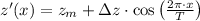
Given that
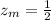 ,
,
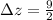 and
and
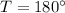 , the outcome is:
, the outcome is:
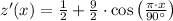
The domain of the function is all real numbers and its range is between -4 and 5. The graph is enclosed below as attachment.