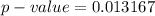Answer:
The p-value is
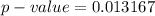
Explanation:
From the question we are told that
The population mean is
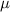 = 200 milligrams
= 200 milligrams
The sample size is
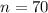
The sample mean is
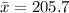
The sample standard deviation is
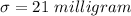
Generally the Null hypothesis is mathematically represented as
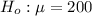
The Alternative hypothesis is
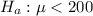
The test statistics is mathematically represented as
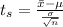
substituting values
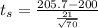
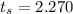
Now the p-value is mathematically represented as
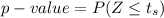
substituting values
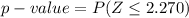
Using the Excel function[=NORMDIST(2.270)] to calculate the p-value we obtain that