Answer:
The probability that the cycle time exceeds 65 minutes if it is known that the cycle time exceeds 55 minutes, should be 1 / 3.
Explanation:
It is known that the cycle times for a truck hauling concrete is uniformly distributed over a time interval of ( 50, 70 ). If c = cycle time, according to the question the probability that the cycle exceeds 65 minutes, respectively exceed 55 minutes should be the following - '
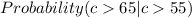 . '
. '
_____
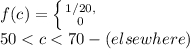
We know that the formula for Probability( A | B ) is P( A ∩ B ) / P( B ),
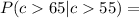
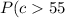 ∩
∩
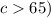 /
/
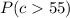 ,
,
And now we come to the formula
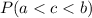 =
=
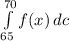 . Substitute known values to derive two solutions, forming a fraction that represents the probability we desire.
. Substitute known values to derive two solutions, forming a fraction that represents the probability we desire.
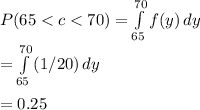
-------------------------------------
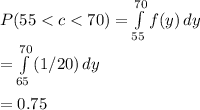
Take 0.25 over 0.75, 0.25 / 0.75, simplified to the fraction 1 / 3, which is our solution.
_____
Probability: 1 / 3