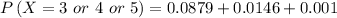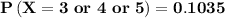Answer:
a
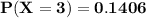
b
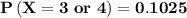
c
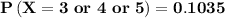
Explanation:
Given that:
In a multiple choice quiz:
there are 5 questions
and 4 choices for each question (a, b, c, d)
let X be the correctly answered question = 1 answer only
and Y be the choices for each question = 4 choices
The probability that Robin guessed the correct answer is:
Probability = n(X)/n(Y)
Probability = 1//4
Probability = 0.25
The probability mass function is :
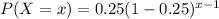
We are to find the required probability that the first question she gets right is the 3rd question.
i.e when x = 3
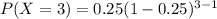
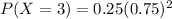
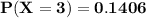
b) Find the probability that She gets exactly 3 or exactly 4 questions right
we know that :
n = 5 questions
Probability P =0.25
Let represent X to be the number of questions guessed correctly i,e 3 or 4
Then; the probability mass function can be written as:
![\[P\left( {X = x} \right) = \left( {\begin{array}{*{20}{c}}\\5\\\\x\\\end{array}} \right){\left( {0.25} \right)^x}{\left( {1 - 0.25} \right)^(5 - x)}\]](https://img.qammunity.org/2021/formulas/mathematics/college/8ia0bd73ibyl7xnndgzvstzg0ffh6by0lk.png)
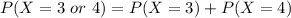
![\[P\left( {X = 3 \ or \ 4 } \right) = \left( {\begin{array}{*{20}{c}}\\5\\\\3\\\end{array}} \right){\left( {0.25} \right)^3}{\left( {1 - 0.25} \right)^(5 - 3)}\] + \left( {\begin{array}{*{20}{c}}\\5\\\\4\\\end{array}} \right){\left( {0.25} \right)^4}{\left( {1 - 0.25} \right)^(5 - 4)}\]](https://img.qammunity.org/2021/formulas/mathematics/college/50jq5atz2dp98db1bzyynhl6wvpaf518kp.png)
![\[P\left( {X = 3 \ or \ 4 } \right) = (5!)/(3!(5-3)!)\right){\left( {0.25} \right)^3}{\left( {1 - 0.25} \right)^(5 - 3)}\] + (5!)/(4!(5-4)!) \right){\left( {0.25} \right)^4}{\left( {1 - 0.25} \right)^(5 - 4)}\]](https://img.qammunity.org/2021/formulas/mathematics/college/9oe91ozyfp6v5g28q88fuo6q0324wyl8vq.png)
![\[P\left( {X = 3 \ or \ 4 } \right) = (5!)/(3!(2)!)\right){\left( {0.25} \right)^3}{\left( {0.75} \right)^(2)}\] + (5!)/(4!(1)!) \right){\left( {0.25} \right)^4}{\left( {0.75} \right)^(1)}\]](https://img.qammunity.org/2021/formulas/mathematics/college/5k3x124ud9l7ttod8h78v4ip1fm7yh0ijz.png)
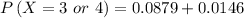
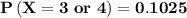
c) Find the probability if She gets the majority of the questions right.
We know that the probability mass function is :
![\[P\left( {X = x} \right) = \left( {\begin{array}{*{20}{c}}\\5\\\\x\\\end{array}} \right){\left( {0.25} \right)^x}{\left( {1 - 0.25} \right)^(5 - x)}\]](https://img.qammunity.org/2021/formulas/mathematics/college/8ia0bd73ibyl7xnndgzvstzg0ffh6by0lk.png)
So; of She gets majority of her answers right ; we have:
The required probability is,
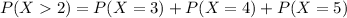
∴
![\[P\left( {X = 3 \ or \ 4 \ or \ 5 } \right) = \left( {\begin{array}{*{20}{c}}\\5\\\\3\\\end{array}} \right){\left( {0.25} \right)^3}{\left( {1 - 0.25} \right)^(5 - 3)}\] + \left( {\begin{array}{*{20}{c}}\\5\\\\4\\\end{array}} \right){\left( {0.25} \right)^4}{\left( {1 - 0.25} \right)^(5 - 4)}\]+ \left( {\begin{array}{*{20}{c}}\\5\\\\5\\\end{array}} \right){\left( {0.25} \right)^5}{\left( {1 - 0.25} \right)^(5 - 5)}\]](https://img.qammunity.org/2021/formulas/mathematics/college/psbyizzuekqtndnq5upe5hvd2hr9jtn5jj.png)
![\[P\left( {X = 3 \ or \ 4 \ or \ 5 } \right) = (5!)/(3!(5-3)!)\right){\left( {0.25} \right)^3}{\left( {1 - 0.25} \right)^(5 - 3)}\] + (5!)/(4!(5-4)!) \right){\left( {0.25} \right)^4}{\left( {1 - 0.25} \right)^(5 - 4)}\] + (5!)/(5!(5-5)!) \right){\left( {0.25} \right)^5}{\left( {1 - 0.25} \right)^(5 - 5)}\]](https://img.qammunity.org/2021/formulas/mathematics/college/yhc7yjxk1d66mq0w8oxheu3ruqmentixbn.png)
![\[P\left( {X = 3 \ or \ 4 \ or \ 5 } \right) = (5!)/(3!(5-3)!)\right){\left( {0.25} \right)^3}{\left( {1 - 0.75} \right)^(2)}\] + (5!)/(4!(5-4)!) \right){\left( {0.25} \right)^4}{\left( {0.75} \right)^(1)}\] + (5!)/(5!(5-5)!) \right){\left( {0.25} \right)^5}{\left( {0.75} \right)^(0)}\]](https://img.qammunity.org/2021/formulas/mathematics/college/aelp4lfu1bdy1pww3s40wbntuo6ocpcfeh.png)