Question

In a random sample of 964 young adults aged 18-29, it was found that 196 of them were married. Construct a 99% confidence interval for the proportion of married young adults aged 18-29.

Answer 1

99% confidence interval for the proportion of married young adults aged 18-29.

(0.1779 , 0.2287)

Explanation:

Step(i):-

Given sample size 'n' = 964

Given data a random sample of 964 young adults aged 18-29, it was found that 196 of them were married

sample proportion

`p^(-) = (196)/(964) = 0.2033`

Step(ii):-

99% confidence interval for the proportion of married young adults aged 18-29.

`(p^(-) - Z_(0.05) \sqrt{(p^(-)(1-p^(-) ) )/(n) } ,p^(-) +Z_(0.05) \sqrt{(p^(-)(1-p^(-) ) )/(n) })`

`(0.2033 -1.96 \sqrt{(0.2033(1-0.2033 ) )/(964) } ,0.2033 +1.96\sqrt{(0.2033(1-0.2033 ) )/(964) })`

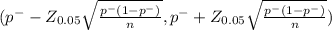
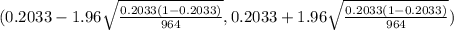
(0.2033 - 0.02540 , 0.2033 +0.02540)

(0.1779 , 0.2287)

Conclusion:-

99% confidence interval for the proportion of married young adults aged 18-29.

(0.1779 , 0.2287)