Answer:
The answer is given below
Explanation:
Given that the location of the points are W = (3, 1) , X = (7, -1), Y = (7, -3) and Z = (3,-3)
The distance between two points A(x1, y1) and B(x2, y2) is given by the formula:
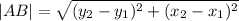
Therefore, the side length of the quadrilaterals are:
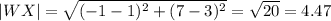
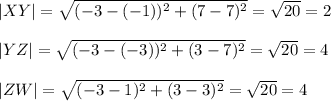
The Perimeter of the quadrilateral = |WX| + |XY| + |YZ| + |ZX| = 4.47 + 2 + 4 + 4 = 14.47 units