Answer:
The coordinates of the point on a circle with radius 4 at an angle of
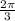 radians are x = -2 and y = 3.464.
radians are x = -2 and y = 3.464.
Explanation:
This problem ask us to determine the rectangular coordinates from polar coordinates. The polar coordinates of the point in rectangular form is expressed by the following expression:
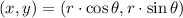
Where
 and
and
 are the radius of the circle and the angle of inclination of the point with respect to horizontal, measured in radians. If
are the radius of the circle and the angle of inclination of the point with respect to horizontal, measured in radians. If
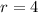 and
and
 , the coordinates of the point are:
, the coordinates of the point are:

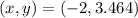
The coordinates of the point on a circle with radius 4 at an angle of
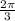 radians are x = -2 and y = 3.464.
radians are x = -2 and y = 3.464.